前言

原文地址：https://xuedongyun.cn/post/11408/

第一题: 小红的数组增值

题目

时间限制: 3000MS
内存限制: 589824KB
题目描述:
小红拿到了一个数组，她准备不断进行如下操作
1、若a_0=0，则直接删除a_0，并将数组其余的所有元素向左移动来填补空缺。
2、否则在数组的未尾添加a_0个a_0-1，然后使得a_0减1。
小红想知道，从开始进行操作直到数组为空，她一共进行了多少次操作？答案请对10^9+7取模。
输入描述

第一行输入一个正整数n，代表数组的长度。
第二行输入n个正整数a_i，代表数组的元素。
1 <= n <= 10^5
1 <= a_i <= 10^5

输出描述

一个整数，代表操作的次数对10^9+7取模的值。

样例输入

2

1 2

样例输出

13

解法

这道题暴力肯定会超时，我们不妨分析一下将数组中一个数彻底消除需要多少步。设数的值为n，将其完全消除需要dp[n]步。n经过1步，变为n+1个n-1。现在有状态转移方程：

dp[n] = (n+1)dp[n-1]+1

最后对数组中所有值求和即可

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

long MOD = 1_000_000_000 + 7;
Integer[] ints = new Integer[]{1, 2, 3};

Integer maxValue = Stream.of(ints).max(Integer::compareTo).get();
long[] dp = new long[maxValue+1];
dp[0] = 1;
for (int i = 1; i <= maxValue; i++) {
    dp[i] = ((i + 1) * dp[i - 1] + 1) % MOD;
}

long result = 0;
for (Integer i : ints) {
    result += dp[i];
}

System.out.println(result);

第三题: 小红的字符串权值

题目

时间限制: 3000MS
内存限制: 589824KB
题目描述:
小红很喜欢’red”字符串，她定义一个字符串的美丽度为: 该字符串包含的”red”子序列的数量。注意子序列是可以不连续的，例
如”rreed”包含了4个”red”子序列，因此美丽度为4。
小红定义一个字符串的权值为: 该字符用所有连续子串的美丽度之和。例如，”redd”的权值为3，因为它包含了一个”red”连续子串，美
丽度为1，包含了一个”redd”连续子串，美丽度为2，其它连续子串的美丽度都为0。
小红想知道，长度为n的、仅由字符’r、’e’、’d”构成的所有字符串(共有3个字符串)的权值之和是多少？答案请对10^9+7取模。
输入描述

一个正整数
1<= n <= 1000

输出描述

长度为n的、仅由字符’r、’e’、’d’构成的所有字符串的权值之和。

样例输入

3

样例输出

1

提示

说明:

长度为3的字符串，仅有”red”权值为1，其余字符串权值为0

解法

这道题有一点绕，刚开始可能理不太清除。我们简单来理理:

• 美丽度: 是一个字符串的属性。即包含”red”子序列的数量(子序列可以不连续)
• 权重: 也是一个字符串的属性。即字符串所有连续子序列的”美丽度”之合

现在我们要求的是: 给定长度n的字符串，所有排列组合可能的”权值”之和。毋庸置疑，这种计算量的题目必定是用动态规划做的。下面分享一下我的做法，我们可以将问题拆分为若干个子问题:

第一步: 给定长度n的字符串，所有排列组合中，会出现多少对”re”(r和e可以不连续)

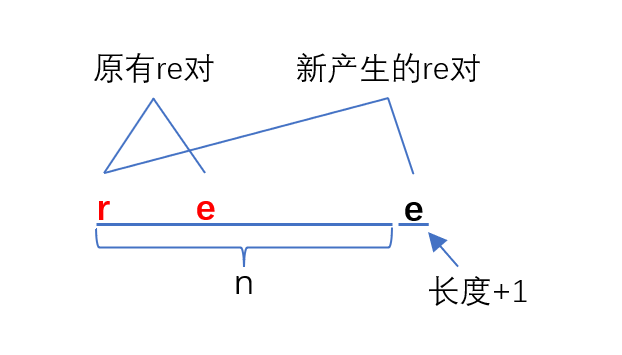
这可以通过动态规划来求，假设re[n]表示长度为n的字符串，所有排列中”re”(可以不连续)出现的次数。那么re[n+1]其实就是在原有”re”对的基础上，增加之前的r搭配后面的e的组合。因此，可以列出状态转移方程:

解释:

• 因为新增了一位(r，e，d三种可能)，所以原有”re”对的数量会翻三倍
• 至于前面的”r”搭配后面的”e”的情况，我们只需要看前面长度为n的序列中能产生多少”r”即可。具体来说，前面n位一共有种排列，每种排列包含n个字母。又因为每个字母出现概率均等，因此”r”出现的次数为

现在我们能计算: 给定长度的序列的所有排列中，能找到多少”re”对

第二步: 给定长度n的字符串，所有排列组合中，会出现多少组”red”(r，e和d可以不连续)

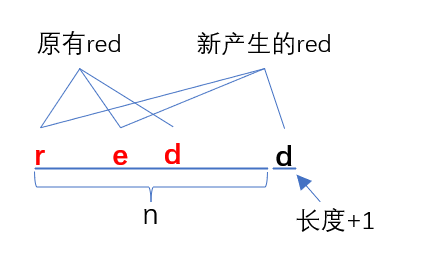
同样的思路，假设red[n]表示长度为n的字符串，所有排列中”red”(可以不连续)出现的次数。给出状态转移方程:

解释:

• 因为新增了一位(r，e，d三种可能)，所以原有”red”的数量会翻三倍
• 如果新增一个”d”，会导致前面”re”加上新增的”d”产生新的”red”

第三步: 给定长度n的字符串，所有排列组合，”权重”之和

我们继续用动态规划的思路来做。我们重点关注多了一位后，会导致所有连续子序列的”美丽度”多多少。

• 考虑一: 原有美丽度会多多少

我们先什么都不管，只考虑在末尾多了一个字母后，原有的所有连续子序列种”red”会变多多少？很明显，由于多了一个字母(r，e，d三种可能)，原有”美丽度会翻三倍”。

考虑一中新增的美丽度:

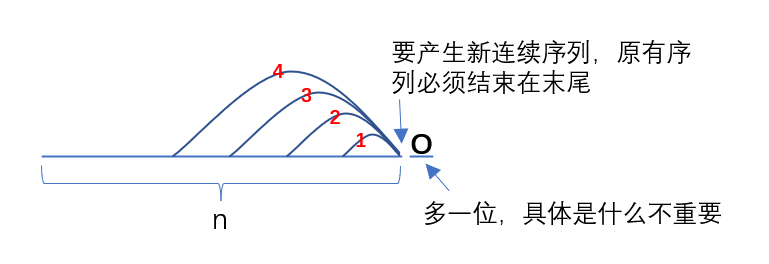
• 考虑二: 现在末尾多了一位，暂时不算它。现在会产生新的连续子序列，导致”美丽度”增加。

增加的”美丽度”其实就是长度为1, 2, 3, 4…n这几个连续子序列中“red”产生的。

举例说明:"red"

连续子序列有: “red”(美丽度1)，因此总权重为1。

多一个”r”，变为"redr"，连续子序列有: “red”(美丽度1)，”redr”(美丽度1)，因此总权重为2。

前后虽然”red”没有变多，但是”美丽度”却变多了，导致权重增加。

举例来说，对于长度为5的，在末尾位置结束的连续子序列，新增美丽度为:，最终所有新增量相加即可。

考虑二中新增的美丽度:

• 考虑三: 末尾多了一位”d”，与前面”re”新组合为”red”，导致”美丽度增多”

和考虑二中思路类似。增加的”美丽度”其实就是长度为1, 2, 3, 4…n这几个连续子序列中“re”产生的。

举例来说，对于长度为5的，在末尾位置结束的连续子序列，新增美丽度为:

考虑三中新增的美丽度:

• 最终我们得到状态转移方程

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

MOD = 10**9 + 7
n = 1000

# 1->0, 2->0, 3->1可以直接返回

# 步骤一
re = [0] * n
re[0] = 0
re[1] = 1
for i in range(2, n):
    re[i] = (3*re[i-1] + 3**(i-1) * i) % MOD

# 步骤二
red = [0] * n
red[2] = 1
for i in range(3, n):
    red[i] = (3*red[i-1] + re[i-1]) % MOD

# 步骤三
dp = [0] * n
dp[0] = 0
dp[1] = 0
dp[2] = 1
for i in range(3, n):
    value = 3 * dp[i-1]
    for j in range(0, i):
        value += 3 * red[j] * 3**(i - j - 1) + re[j] * 3**(i - j - 1)
        value = value % MOD
    dp[i] = value

print(dp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int n = 1000;
int MOD = 1_000_000_000 + 7;
BigInteger MOD_BIG = BigInteger.valueOf(MOD);

// 1->0, 2->0, 3->1可以直接返回

// 步骤1
long[] re = new long[n];
re[1] = 1;
for (int i = 2; i < n; i++) {
    re[i] = (3 * re[i - 1] + i * BigInteger.valueOf(3).pow(i - 1).mod(MOD_BIG).longValue()) % MOD;
}

// 步骤2
long[] red = new long[n];
red[2] = 1;
for (int i = 3; i < n; i++) {
    red[i] = ((3 * red[i - 1]) % MOD + re[i - 1]) % MOD;
}

// 步骤三
long[] dp = new long[n];
dp[2] = 1;
for (int i = 3; i < n; i++) {
    dp[i] = 3 * dp[i-1];
    for (int j = 1; j < i; j++) {
        dp[i] += ((3 * red[j] + re[j]) % MOD) * BigInteger.valueOf(3).pow(i - j - 1).mod(MOD_BIG).longValue();
        dp[i] = dp[i] % MOD;
    }
}

System.out.println(dp[n - 1]);

更优解法

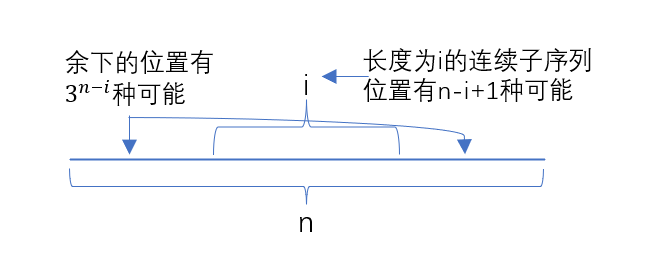
仔细思考后发现一个更优解法。我们之前其实已经能拿到red[i]，那么对于一个长度为n的任意排列的序列来说，其中长度为i的连续序列产生的”美丽度”就应当为：

解释：

长度为i的连续子序列，所有排列中的”美丽度”总和red[i]在上一个解法，我们已详细探讨。

现在，剩下的个位置一共有种可能

同时，这个长度为i的连续子序列的位置未知，一共有种可能

我们现在只需要遍历i，最后求和就可以了

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

MOD = 10**9 + 7
n = 1000

# 1->0, 2->0, 3->1可以直接返回

# 步骤一
re = [0] * n    
re[1] = 1
for i in range(2, n):
    re[i] = (3*re[i-1] + 3**(i-1) * i) % MOD

# 步骤二
red = [0] * n
red[2] = 1
for i in range(3, n):
    red[i] = (3*red[i-1] + re[i-1]) % MOD

# 步骤三
result = 0
for i in range(1, n):
    result = (result + red[i] * 3**(n-i-1) * (n - i)) % MOD
print(result)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

int n = 1000;
int MOD = 1_000_000_000 + 7;
BigInteger MOD_BIG = BigInteger.valueOf(MOD);

// 1->0, 2->0, 3->1可以直接返回

// 步骤1
long[] re = new long[n];
re[1] = 1;
for (int i = 2; i < n; i++) {
    re[i] = (3 * re[i - 1] + i * BigInteger.valueOf(3).pow(i - 1).mod(MOD_BIG).longValue()) % MOD;
}

// 步骤2
long[] red = new long[n];
red[2] = 1;
for (int i = 3; i < n; i++) {
    red[i] = ((3 * red[i - 1]) % MOD + re[i - 1]) % MOD;
}

// 步骤三
long result = 0;
for (int i = 0; i < n; i++) {
    long temp = (red[i] * (n - i)) % MOD;
    temp = (temp * BigInteger.valueOf(3).pow(n - i - 1).mod(MOD_BIG).longValue()) % MOD;
    result += temp;
    result %= MOD;
}

System.out.println(result);